在基线通过重复基线较差、异步环闭合差、三维无约束平差基线向量改正数（粗差检验）等基线质量指标检核后，表明基线质量合格，可以进行平差计算。本文重点对GSP软件的无约束平差计算做详细介绍，约束平差计算将在下一篇文章《GSP软件对基线的约束平差计算》 进行介绍，平差后的精度评定以《高速铁路工程测量规范》为例进行说明。
平差计算主要分为无约束平差和约束平差两个过程，三维无约束平差主要检核基线内符合精度，通过三维无约束平差计算可以得到基线向量各分量的改正数，GSP软件可以快速的检查是否存在粗差。
三维无约束平差可用一个点的准确坐标或者单点定位的大地坐标作为起算点，在GSP软件中的“k已知参数”中表格中输入三维起算点的坐标，如图1标号4所示。
图1 GSP软件中输入已知参数信息
图1输入的是起算点的大地坐标BLH，其中BL格式为度分秒，也可输入空间直角坐标XYZ格式。GSP软件能自动识别输入的三维坐标是属于大地坐标还是空间直角坐标。可在表格中手动输入起算点的三维坐标，也可以直接导入坐标，GSP提供2种方式导入坐标：1、文本导入坐标；2、剪贴板导入坐标。如图1蓝色字体所示，“文件导入坐标”按钮实现的功能是打开存放了坐标的文本文件，从文本文件中读取坐标，“剪贴板导入坐标”按钮实现的功能是将复制到剪贴板内存中的坐标导入到图1所示的表格里。图1所示的已知参数信息还包括椭球参数、中央子午线经度、投影面大地高。在图1标号1所示的椭球参数表格中，可设置椭球参数。GSP默认是WGS84椭球，如果需要修改，鼠标单击WGS84表格，会出现下拉选项，如图2所示。
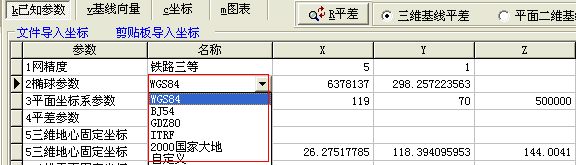
图2 GSP软件设置椭球参数类型
GSP软件提供了常用的几种椭球参数：WGS84、BJ54(北京54椭球)、GDZ80（西安80椭球）、ITRF(国际大地参考坐标系)、2000国家大地坐标系（中国国家测绘局推广今后使用）以及自定义椭球，自定义椭球需要修改设置椭球长半轴参数以及扁率分母，在“椭球参数”这一行进行修改设置。
GSP软件具有自动提示功能，当不清楚表格栏应该输入的参数格式和内容时，只需要鼠标移到表格里，就可得到相应提示，这个功能很方便智能，是CosaGPS等软件不具备的功能。
在图1所示的GSP软件已知参数信息，标号2和标号3所在的表格分别输入中央子午线经度和投影面大地高，本例的中央子午线经度：119度，投影面大地高：70m。在输入了已知参数信息后，基线可进行三维无约束平差计算。此时基线已通过基线的质量检核，确认基线已经合格。
在平差方式中选择“三维基线平差”
，点击平差计算按钮
，，GSP软件即可完成三维无约束平差计算。基线向量改正数信息显示在“v基线向量”的“3维向量”表格里，如图3所示。
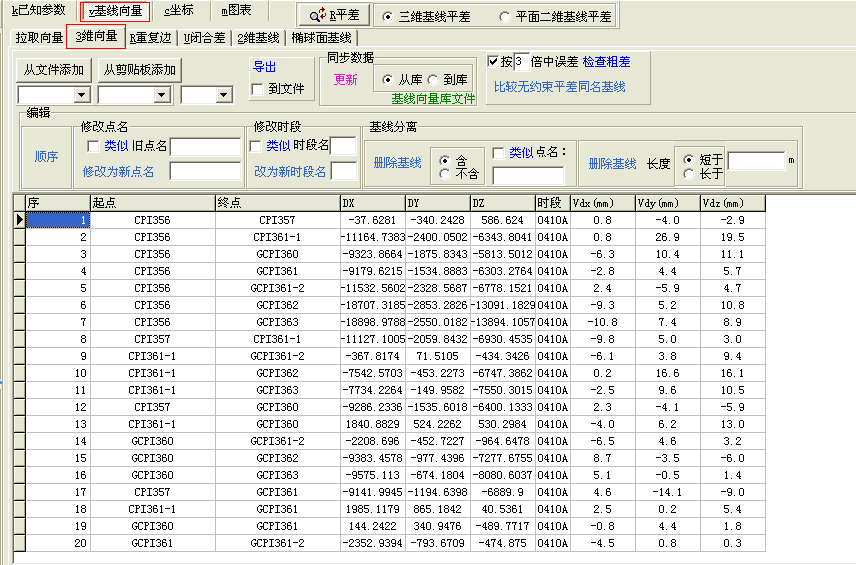
图3 GSP软件无约束平差计算得到的基线向量改正数
点击“检查粗差”按钮可以检查基线是否存在粗差。GSP在进行三维无约束平差计算后，会得到一些计算内容。主要包括：地心坐标及平差精度、大地坐标。其中地心坐标是以已知参数中输入起算点的三维坐标为基准计算得到所有点的空间直角坐标，大地坐标是通过空间坐标转换将计算得出的空间直角坐标转换为大地坐标。GSP软件显示地心坐标和大地坐标的计算表格分别如图4和图5所示。
图4 GSP软件无约束平差计算得出地心坐标及精度信息
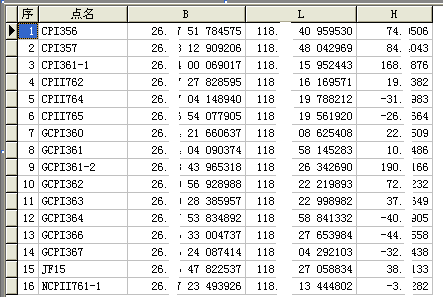
图5 GSP软件无约束平差计算得出大地坐标（BL单位：度分秒）
如果在三维无约束平差计算前，在“k已知参数”页面设置选项勾选“转换到高斯平面G”，如图6所示。
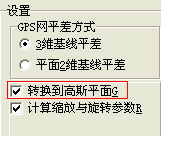
图6 GSP设置无约束平差计算结果转换到高斯平面
GSP软件可以将无约束平差计算的结果转换到给定中央子午线和投影面大地高的高斯平面上，可计算出高斯平面坐标和距离方位误差等信息。如图7和图8所示。
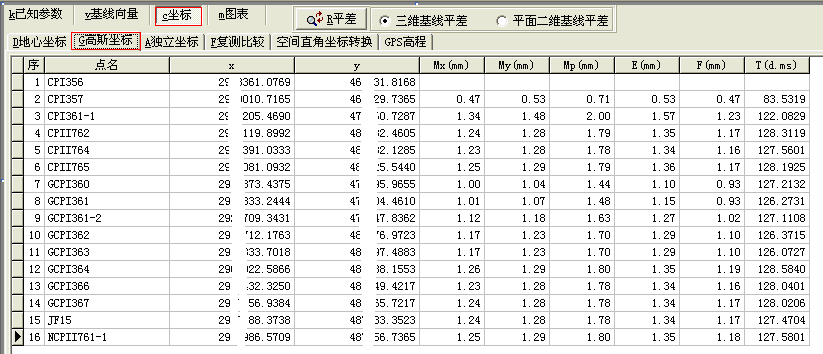
图7 无约束平差计算结果转换到高斯平面得到的高斯平面坐标
图8 无约束平差计算结果转换到高斯平面得到的距离方位误差
若需要显示点位相对误差，则在图8所示的界面中选择“点位相对误差”单选按钮，则可得到点位相对误差信息。这里不作详述。
无约束平差计算后，GSP软件下端的提示栏会显示一些平差信息，包括点的个数、基线观测数量、单位权中误差等，如图9所示。
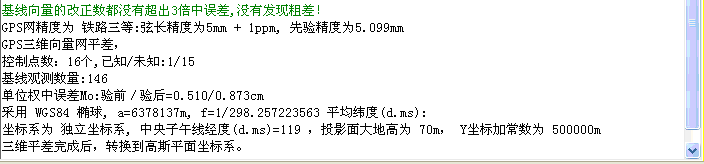
图9 三维无约束平差后的GSP软件显示的平差信息
通过GSP软件计算得到的三维无约束平差结果，可以初步判断基线内符合精度，基线是否存在粗差。在三维无约束平差计算完毕后，可以进行约束平差。
约束平差无论是采用三维约束平差还是二维约束平差，都涉及到选取约束点的问题，一般而言，选择约束点应该遵循“点位稳定、分布均匀、首尾兼顾”等原则，以工程中常用的GPS复测控制网为例，GSP软件提供了一种功能可快速选择稳定可靠的控制点作为约束点，即通过自由网拟稳变换，采用复测控制网的重心和原测控制网的重心基准保持一致的情况下，通过自由网变换后的复测坐标与原测控制网坐标进行比较，在网形基本一致的情况下，坐标较差较小的就可认为点位稳定可靠，可以选作约束点。
GSP软件中自由网变换的操作过程如下。点击按钮“c坐标”——“F复测比较”，如图10所示。
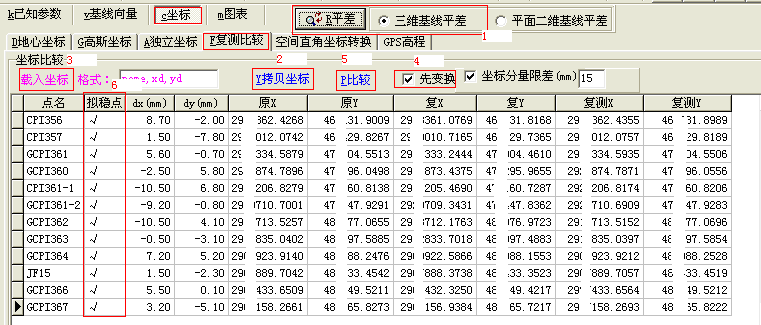
图10 GSP软件通过自由网变换选取约束点
图10所示标号1中的平差方式选择“三维基线平差”，此时自由网拟稳变换指的是通过无约束平差计算得到的高斯坐标和原测坐标之间的变换，选取约束点后才能进行约束平差，点击图10所示标号2“Y拷贝坐标”按钮，将无约束平差计算得到的高斯平面坐标导入到表格中的“复X”、“复Y”栏里，将原测坐标拷贝到剪贴板后，点击标号3所示“载入坐标”按钮，可将原测坐标导入到表格中的“原X”、“原Y”栏里，然后在标号6所示的“拟稳点”选择，初次计算时应全选所有点作为拟稳点，勾选标号4中的“先变换”选项，点击标号5中的“P比较”按钮，就可计算得出自由网变换后的坐标，显示在“复测X”、“复测Y”栏里，以及坐标较差，显示在“dx(mm)”、“dy(mm)”栏里。如图10所示，若发现个别点坐标较差很大，应设置让其不作为拟稳点，重新按上述步骤计算，得到自由网拟稳变换后的结果。通过GSP软件进行自由网拟稳变换，可以顺利的找出稳定可靠的点作为约束点，如图10所示，可选择CPI356、JF15、GCPI360等3个点作为约束点，3点相邻点间坐标差之差的相对精度在GSP的“距离方位比较”表格中可以显示，如图11所示。
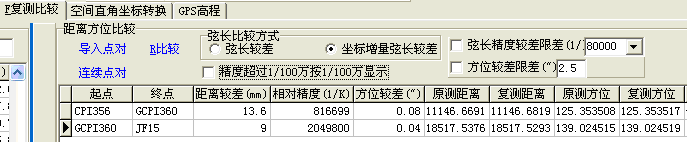
图11 GSP软件计算相邻点间的坐标差之差的相对精度
相邻点间坐标差之差的相对精度计算结果显示如图11所示。可以看出，相对精度很高，完全能满足要求，CPI356、JF15、GCPI360这3点可以作为约束点进行约束平差。
本文重点介绍GSP软件中无约束平差计算的操作过程，在无约束平差计算完毕后，选定了稳定可靠的约束点，就可以进行约束平差计算。GSP对约束平差的计算过程介绍请见下一篇文章《GSP软件对基线的约束平差计算》。
