当需要将不同基准(参考椭球)的坐标相互转换时,例如54椭球的坐标转换为WGS-84椭球坐标、或在RTK测量中计算坐标转换参数时,可以利用GSP的空间直角坐标转换功能。 平面坐标平移旋转参见这里
利用GSP可以
-
通过计算两个空间直角坐标系间的转换参数,也可以直接利用转换参数进行坐标转换。
-
转换参数计算可以选用布尔莎模型或莫洛金斯基模型,
-
可以选用计算出3个平移、3个旋转和1个尺度的7参数或计算3个旋转和1个尺度的4参数模型。
利用3个及以上公共点时,采用最小二乘平差方法按等权方式计算转换参数,同时计算出单位权中误差,及每个转换点的转换误差。
4参数计算,是以第一个点为基准,计算到其他点的坐标增量,然后再计算旋转参数与尺度参数。
布尔莎模型与莫洛金斯基模型转换参数中仅平移参数不同(因旋转中心不同),当然由于计算原因可能出现旋转和尺度参数有微小差异。
莫洛金斯基模型的转换中心采用网的重心。
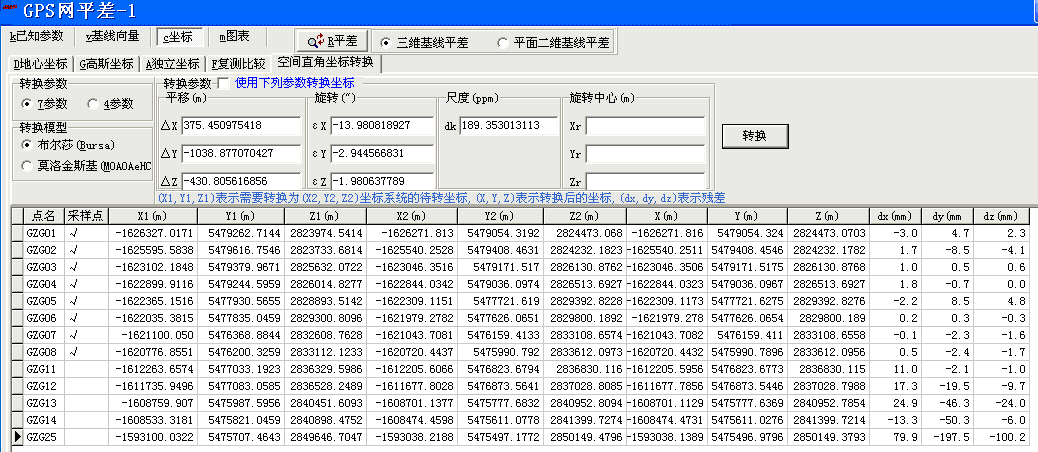
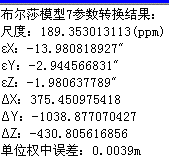
计算时,首先导入或输入公共点的两套空间直角坐标和需要转换的其他点的坐标,公共点的点数需要2个以上,然后在表格中选择公共点为采样点,选择转换参数个数和模型,单击“转换”按钮,GSP将首先计算出转换参数,然后利用转换参数计算转换坐标,并将公共点的转换坐标残差计算出来。
当有转换参数时,可以将转换参数先输入,并选择“使用下列参数转换坐标”选项,单击“转换”按钮,即可完成坐标的转换工作。

提示:
1) 如果是大地坐标请利用GSP转换成空间直角坐标。
2) 在RTK测量中计算7参数时,可以先将地面平面坐标转换为大地坐标,采用正常高代替大地高,再转换成空间直角坐标,然后进行转换参数计算,对WGS-84坐标进行转换后将会是正常高结果。

